MIRTE

Axe Société

Mathématiques
∩ Économie

Aperçu

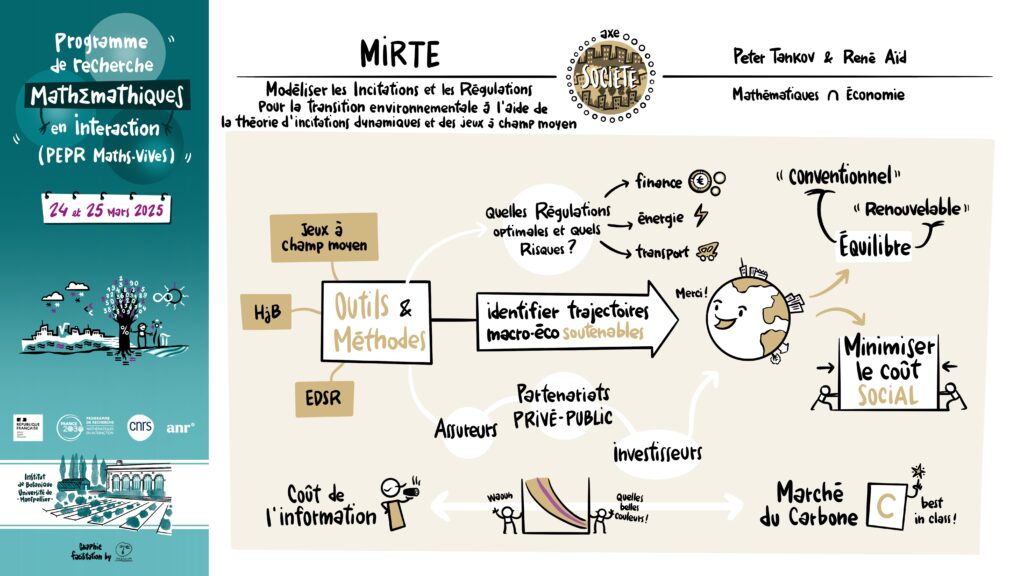
Modéliser les incitations et les régulations pour la transition environnementale à l’aide de la théorie d’incitations dynamiques et des jeux à champ moyen.

Mots clefs

Transition environnementale, risques financiers climatiques, théorie des incitations, jeux à champ moyen

Coordination  

• Peter Tankov (Mathématiques, Centre de Recherche en Economie et Stastistique (CREST), UMR 9194, CNRS, École polytechnique, Groupe des Écoles Nationales d’Économie et Statistique (GENES), Ecole Nationale de Statistique et de l’Administration Economique (ENSAE))
• René Aïd (Économie, Laboratoire d’Economie de Dauphine (LEDA), UMR 8007, CNRS, IRD, Université Paris Dauphine-PSL)

Financement

• ≈ 1 million d’euros sur 5 ans

Résumé

Le projet ciblé MIRTE vise à développer des outils numériques et des méthodes théoriques nouveaux, à l’intersection de la théorie des incitations dynamiques et des jeux à champ moyen. Ces outils et méthodes visent à déterminer les régulations optimales des secteurs essentiels comme la finance, l’énergie et le transport et permettre d’identifier les trajectoires macroéconomiques soutenables. Pour réussir la transition climatique, les puissances publiques doivent réguler les marchés de manière optimale, anticiper la réponse des agents socio-économiques, optimiser les leviers incitatifs et mesurer et contrôler les risques associés. 

Avec les outils récemment développés du contrôle robuste, le projet analysera les risques associés aux différentes régulations en univers incertain. Le projet est organisé autour de trois axes de recherche: (A) les mathématiques des incitations collectives, (B) les mécanismes de marchés pour la transition environnementale et (C) la régulation et la gestion des risques financiers associés à la transition environnementale.

Dans (A), il s’agit d’étendre les méthodes connues à des situations non couvertes par la théorie actuelle mais nécessaires pour aborder les questions d’adaptation au changement climatique (incertitude sur la nature du problème des agents, non-cohérence temporelle).

Dans (B), il s’agit de concevoir les mécanismes décentralisés ainsi que les régulations appropriées pour permettre une meilleure allocation des efforts d’adaptation et de réduction des émissions. Des solutions fondées sur les marchés de permis d’émission avec des allocations dynamiques seront étudiées aux côtés de mécanismes plus intégrées. Ces derniers permettront de comprendre l’exposition aux risques des différents acteurs au sein des systèmes énergétiques.

Dans (C), il s’agit de comprendre et de modéliser les risques financiers potentiellement systémiques qui sont induits par le changement climatique, à la fois dans sa dimension de risque physique mais aussi de risque de transition. En particulier, il s’agit de comprendre comment les pertes de valeur des actifs carbonés peuvent se propager dans le système financier. Cette compréhension a pour but de mettre en place à la fois des stratégies de couverture de risques pour les acteurs exposés, mais aussi des régulations adaptées qui permettent de réduire les risques systémiques.